어읽로꾸거
[수학] 2의 보수, 1의 보수 (+ 왜 필요한지 이유) 본문
r진법, N은 숫자, n자리수
1. r-1의 보수 (2진법의 경우 1의 보수)

r-1의 보수. 2진법과 10진법을 예로 들면 이렇다.
| 원래 수(2진법) | 1의 보수 |
| 101101 | 010010 |
| 100001010 | 011110101 |
| 원래 수(10진법) | 9의 보수 |
| 1234 | 8765 |
| 89023 | 10976 |
특징)
1. 원래수와 r-1의 보수의 자리수마다 더하면 r-1이 됨
2. r의 보수(2진법의 경우 2의 보수)
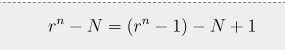
r의 보수. 2진법과 10진법을 예로 들면 이렇다.
| 원래 수(2진법) | 2의 보수 |
| 101101 | 010011 |
| 100001010 | 011110110 |
| 111000 | 001000 |
| 원래 수(10진법) | 10의 보수 |
| 1234 | 8766 |
| 89023 | 10977 |
| 123000 | 877000 |
r-1의 보수와의 차이점은 1만큼 차이가 난다. 따라서 r-1의 보수에 1을 더해주면 r의 보수가 된다. (직관적인데?)
근데 이게 꼼수 특징이 뭐냐면 뒤에서부터 해서 가장 먼저 0이 아닌숫자를 발견하면 해당 자리 숫자를 더해서 r이 되게 만들고 그 앞의 자리는 r-1이 되게 하면 된다.
예를 들면, 10진법 기준으로 다음과 같다.
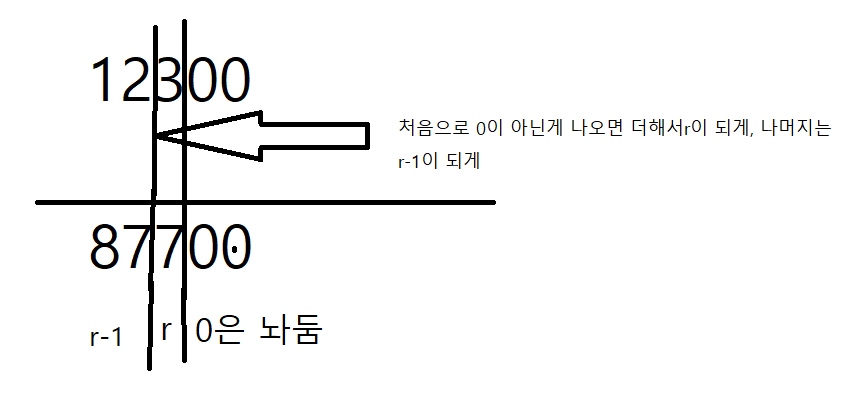
이런 방식이 있다. 별로 어려운건 아니니까 그냥 정직하게 r-1의 보수 구해서 1더해줘도 된다.
특징)
1. r-1의 보수에 1을 더해주면 r의 보수가 됨
2. 오른쪽부터 해서 처음으로 0이 아닌게 나오면 그건 더해서 r이 되게, 나머지는 r-1이 되게 해주면 간단
보수를 그래서 왜 배우냐?
1. (Unsigned 에서)뺄셈을 덧셈으로 표현하기
2. 양수 <=> 음수 컴퓨터에서 바꾸기(2진수에서 2의 보수일때만)
우선 (Unsigned 에서)뺄셈을 덧샘으로 바꿔보자
예를 들어 M-N을 한다고 하자. 이때 M + (N의 2의 보수)를 한다고 하자. 그러면

여기서 2가지 경우로 나뉜다.
1) M >= N인 경우
이때는 r^n을 빼주면 된다. 그러면 그냥 M-N되서 원래 구하려던거 구함
2) M<N인 경우
이때는 좀 복잡하다.

이거 다음에 N-M을 Z라고 치환하자. 그러면

Z의 2의 보수가 된다. 보수의 보수는 원래의 수이므로 해당 수에 대해 2의 보수를 취해주면?

원래 구하려던 M-N에 마이너스를 취한 값이 나온다. 그러면 -(M-N)이 나온다.
따라서 M+(N의 보수)한 값의 보수를 구한 뒤 마이너스를 붙여주면 된다.
아직 미완성
'정리' 카테고리의 다른 글
| [네트워크 프로그래밍] 2. Stream - InputStream (0) | 2022.09.13 |
|---|---|
| [네트워크 프로그래밍] 1. Stream - OutputStream (0) | 2022.09.07 |
| [Python] Fast Api 에서 Eureka 연결하기 (0) | 2022.08.27 |
| [Python] Celery Execution Pools 셀러리 풀에 관하여 (0) | 2022.08.24 |
| [Javascript] 알아야 할 7가지 자료형 (0) | 2020.11.09 |
